PROJECTION OF POINTS
Let us consider a horizontal plane and vertical plane situated as shown in Fig. 6.0. They are forming four quadrants namely:
(1) First quadrant
(ii) Second quadrant
(iii) Third quadrant and
(iv) Fourth quadrant.

1. First Quadrant: It is a space derived above the H.P and in front of V.P as shown in Fig. (a). (The first 90º) observed from the direction of vision for EV.
2. Second Quadrant: The space above H.P and behind V.P is called Second Quadrant (The second 90°) observed from the direction of vision for EV.
3. Third Quadrant: The space under the H.P and behind V.P is known as third quadrant. (The third 90°) observed from the direction of vision for EV.
4. Fourth Quadrant: The space under the H.P and in front of V.P is termed as fourth
quadrant. (The fourth 90°) observed from the direction of vision for F.V.
FRONT VIEW [ELEVATION]
The projection of the object on vertical plane (V.P), when the object is kept in the space of quadrant and viewed from the direction of vision i.e., from front is known as front view [EV] or elevation.
Top View [Plan]
The projection of the object on to the horizontal plane when the object is kept in the space of the quadrants and viewed from the direction of vision from top is known as top view (T.V) plan.
NOTE: For drawing the above views (front view and top views) on the drawing sheet, it is presumed that the intersection of V.P and H.P forms a line say x-y. And with reference to this x-y line the two views are drawn and the H.P should be turned in clockwise direction to observe from the direction of vision from front.
The following examples can give the concept of the concemed projections.
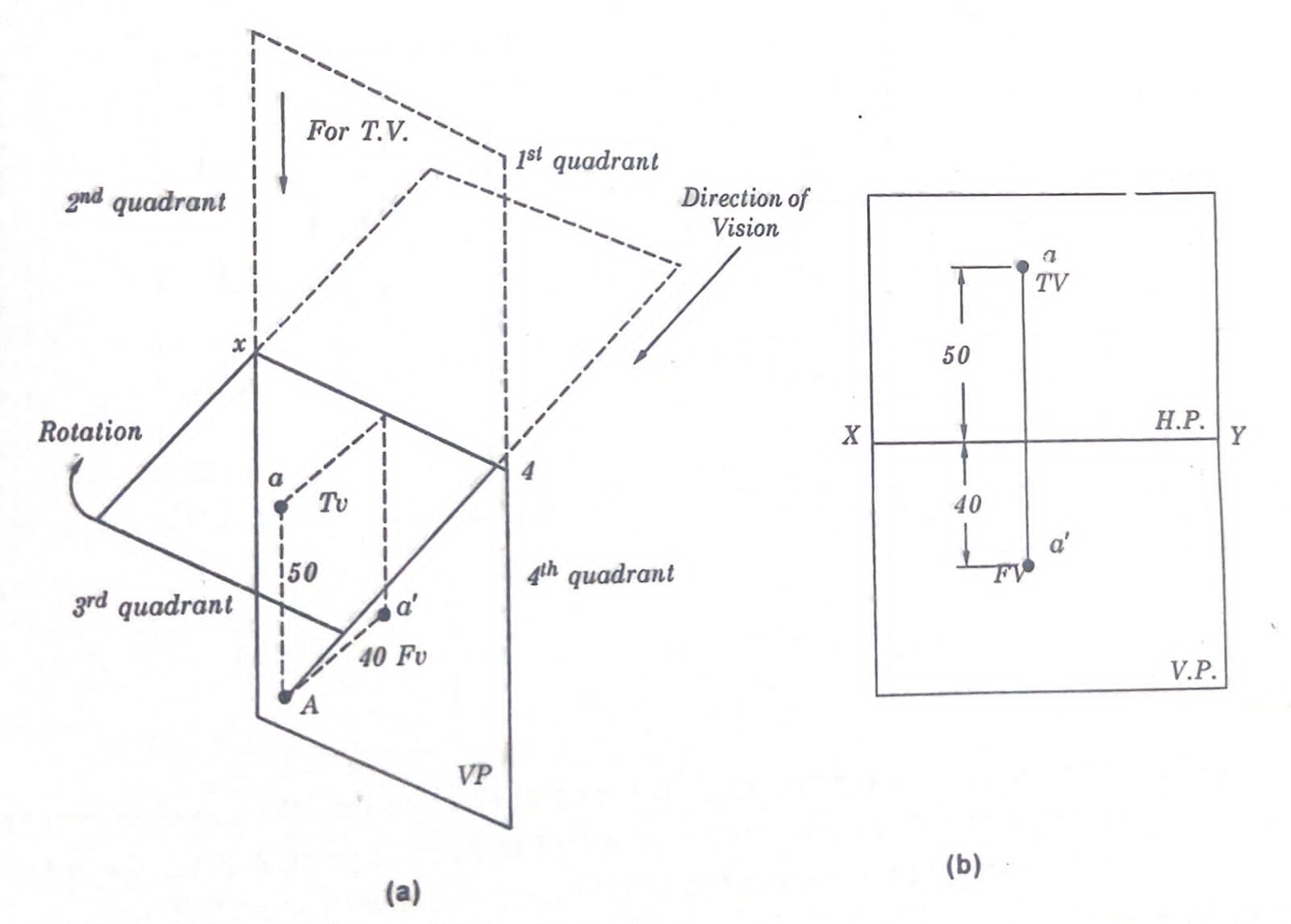
WHEN THE POINT IS IN THE 1S QUADRANT
Q.Draw the projections of a point when it is 40 mm above the Horizontal plane and 25 mm in front of the vertical plane.
Solution:
As the point is in the first quadrant, the concerned views can be drawn as shown below

Here “A” is actual point in the space of a first quadrant a’ and a are the concerned projections on to V.P and H.P respectively. After getting the H.P on par with V.P by rotating clockwise, the projections of point A can be seen as Fig. (b).
WHEN THE POINT IS 2ND QUADRANT
Q.Draw the two views of a point “P” which is 40 mm above H.P and 25 mm behind V.P
Solution:
As the point is in the second quadrant, the concerned views can be understood from Fig. (a) and drawn as in Fig. (b).
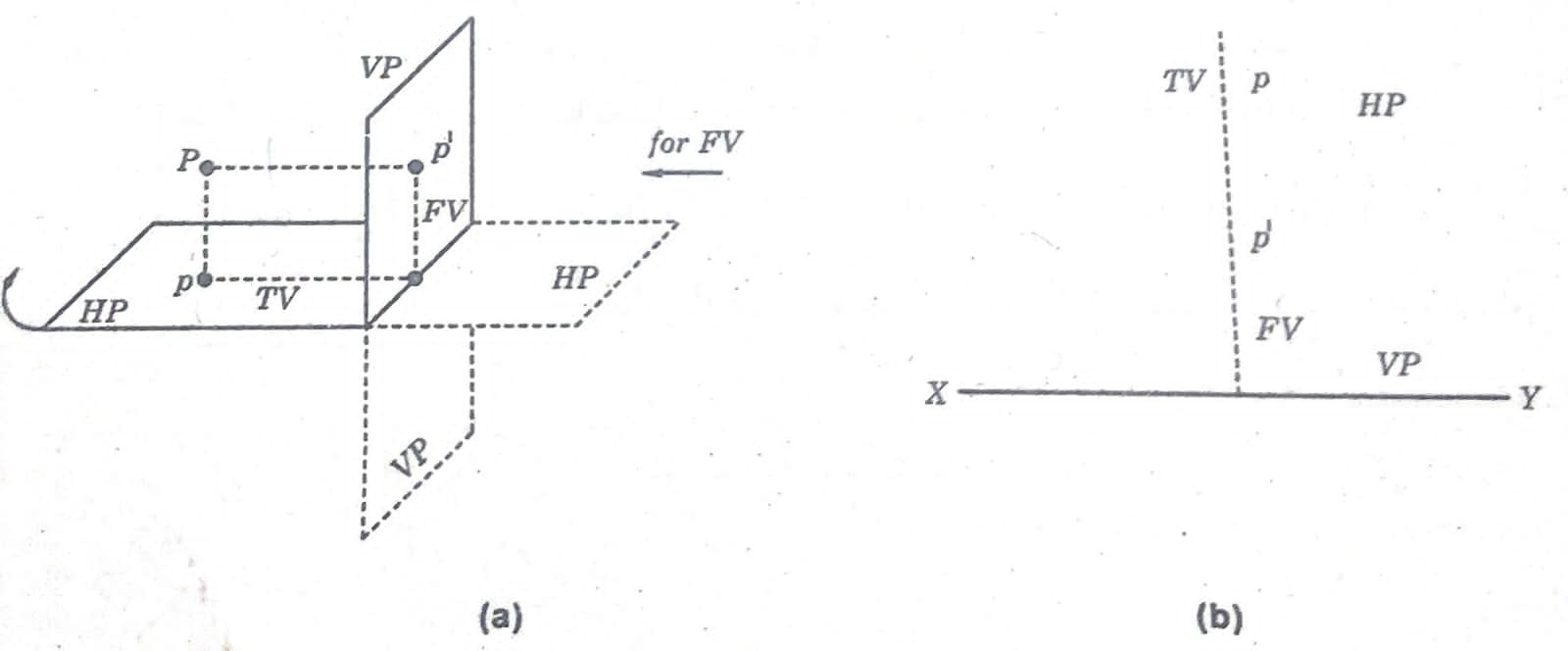
Here “P” is actual point in the space of the second quadrant. p and Pare the concerned projections on to V.P and H.P respectively. After getting H.P on par with V.P by rotating clockwise, the projections P and P of point P can be seen as Fig. (b). Here it is clear that the two views are on the same side of x-y line.
WHEN THE POINT IS IN 3D QUADRANT
Q.A point “A” is lying at 40 mm behind V.Pand 50 mm below H.P. Draw its projections.
Solution:
Here “A” is the actual point in space as shown in Fig. (a) a’ and a are the concerned projections on the V.P and H.P respectively. After rotating H.P clockwise the projections a and a’ of “A” can be seen as in Fig. (b). In this case the H.P after rotating appear over x-y line i.e., quite opposite to that of the projections of the object in the first quadrant.
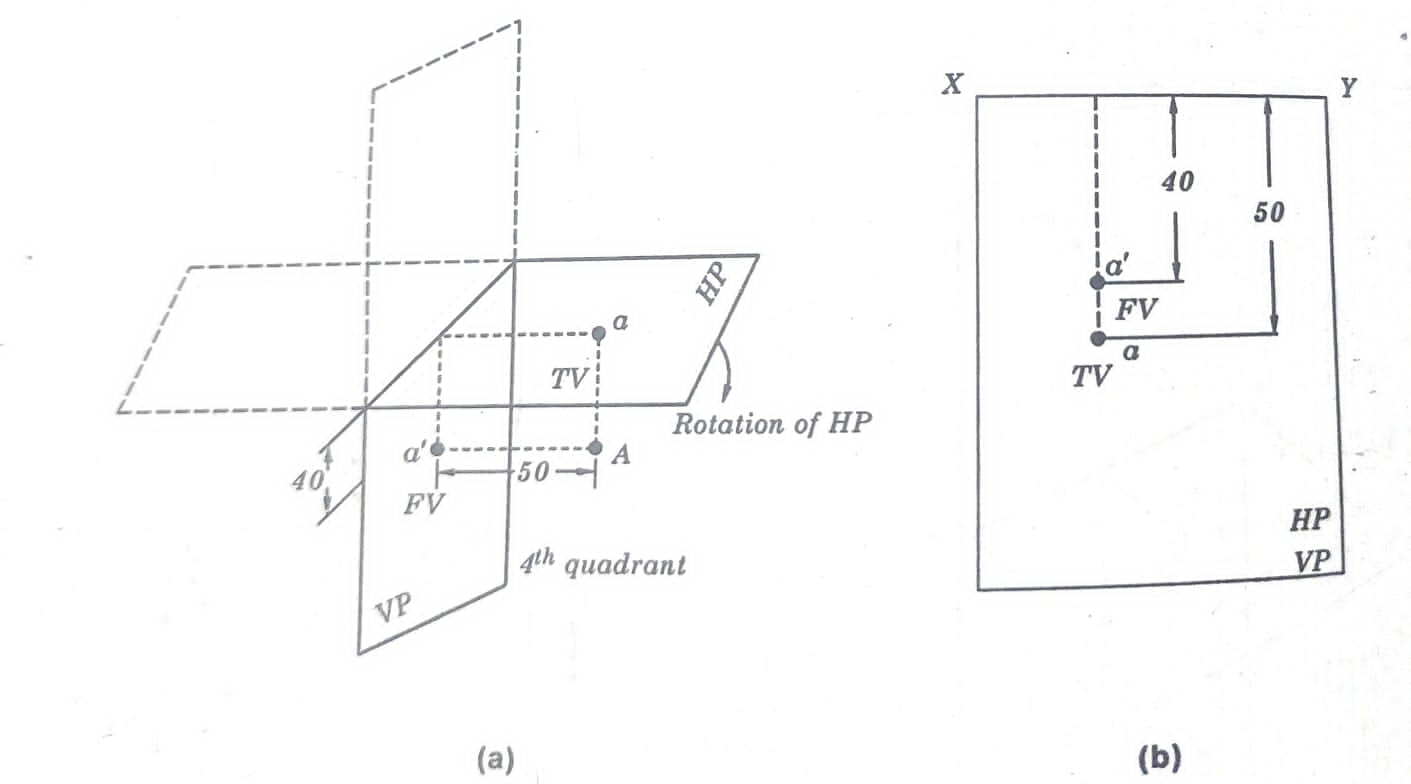
WHEN THE POINT IS IN THE 4TH QUADRANT
Q. Draw the projections of point “A” which lies 40 mm under the H.P and 50 mm in front of the V.P
Solution:
The point “A” is lying in the fourth quadrant and the concerned projections are quite opposite to the projections of the object in the second quadrant Fig. (a & b).