STRENGTH OF MATERIAL

A simply supported beam of 6m span carries a udl of 10 kN/m over the left support 2 m length and also carries point loads of 15 kN acts at a distances of 4 m respectively from left support. Find the support reactions.

by

  SOLUTIONS: Total load= 10×2+15= 35kN Taking moments about A RB×6 = 15×4+ (10×2) 2/2 RB×6 = 80 RB = 80/6 = 13.33kN RA = Total load – RB RA= 35 -13.33 = 21.67kN

Q.A Simply Supported beam of length 4 m carries two point loads of 50 kN and 100 kN are placed at a distance of 1 m and 3 m from the left hand support. Find the reactions.

by

  SOLUTION : Total load  =50+100= 150kN Taking moments about A RB x 4 = 50 x 1 + 100 x 3 RB x 4 = 350 RB= 350/4 = 87.5kN RA= Total load – RB RA= 150 – 87.5 = 62.5kN ( or) Taking moments about B RA x 4 = 100×1 +50×3 RA … Read more

A simply supported beam of 6m span carries a udl of 4 kN/m over the middle 2 m length and also carries point loads of 2 kN and 4 kN acts at a distances of 1 m and 5 m respectively from left support. Find the support reactions.

by

SOLUTION : Total load = 2+4+4×2= 14kN Taking moments about. A RB x 6 = 2 x 1+4×5+(4×2) ( 2 / 2+2) RB x 6= 46 RB= 46 / 6 = 7.67kN RA = Total load – RB  RA= 14 – 7.67= 6.33kN ( or ) Taking moments about B RA x 6 = 4×1+2×5+(4×2) … Read more

A simply supported beam of span 4 m carries a udl of 10 kN/m over the entire span and a point load of 10 kN acting at distance of 1m from let end. Find the reactions at supports.

by

SOLUTION : Total load = 10 x 4 + 10 = 50 Taking moments about A RB x 4 = 10 x 1 + ( 10×4 ) 4/2 RB x 4 = 90kN RB = 90 / 4 = 22.5kN RA= Total load – RB RA= 50 – 22.5 = 27.5kN ( or ) Taking … Read more

A beam of length 8 m carries two point loads of 60 kN and 90 kN are placed at a distance of 3 m and 5 m from the left hand support. Find the reactions.

by

SOLUTION : Total Load = 60+90= 150kN Taking moments about A RB×8 = 60×3 + 90 x 5 RB x 8 = 630 RB = 630/8 = 78.75kN RA = Total load – RB RA= 150 – 78.75  = 71.25kN ( or ) Taking moments about B RA x 8 = 90×3 + 60×5 RA … Read more

A simply supported beam of span 4 m carries a point load 10 kN at a distance of 1 m from left support. Find the reactions at the supports

by

SOLUTION: Total load = 10kN Taking moments about A RB ×4=10×1 RB= 10 / 4 = 2.5kN RA= 10 – 2.5 = 7.5kN Taking moments about B’ RA x 4= 10 x 3 RA = 30/4 = 7.5 kN

A simply supported beam of 4 m span carries a point load of 10kN at its centre. Find the reactions at the supports.

by

A simply supported beam of 4 m span carries a point load of 10kN at its centre. Find the reactions at the supports. Solution: The load applied symmetrical. Hence  RA = RB = Total load/2                 = 10 / 2                 … Read more

SHEAR FORCE AND BENDING MOMENT DIAGRAM

by

SHEAR FORCE AND BENDING MOMENT DIAGRAM

SHEARFORCE AND BENDINGMOMENT DIAGRAM        Shear Force: The shear force at any section of a beam is equal to the algebraic sum of all the forces either to the left or to the right of the section. S.F is denoted by the letter F and its units in Sl are kN.

The beam may also state the unbalanced vertical force to the left or right of the section at the cross-section.

Sign Convention For Shear Force

We find different sign conventions in different books, but in this book we follow this sign convention in the entire book.

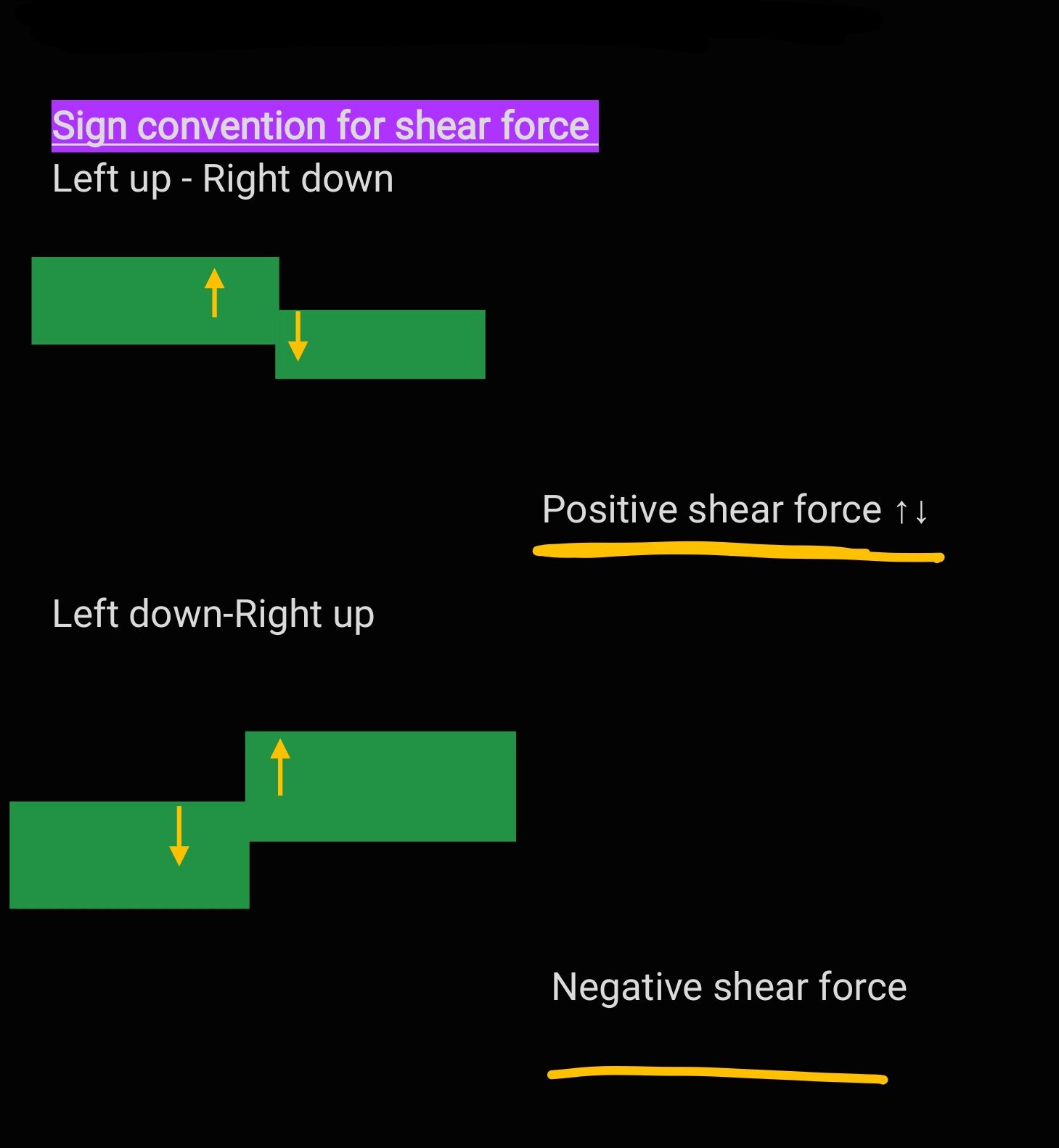
Shear Force Diagram:

The shear force plotted as ordinate on the base line representing the axis of the beam is known as SFD.

Procedure to be Followed for Drawing SFD:1. Draw the loading diagram of the beam.

2. Find reactions of the support and draw lines below loading points

3. Start always from left side of the beam as per the los whether it is up or down ward and continue till right.enc of the beam.
4. By the time it reaches right end it has to reach zero of the base line otherwise your reactions calculations may be wrong or loading calculations may be wrong correct it immediately

5. Positive values are plotted above the base line and fiegative values below the base line and hatch it properly and indicate + ve and -ve.

6. Mention the values of shear force at each corner of the diagram.

7 Find the maximum positive shear force and minimum negative shear force values.

8. Where shear force crosses +ve to -ve or vice versa the B.M will be maximum at those points

9. At some place it crosses base line not at nodal point especially under ud! Find x distance where it crosses base line by using similar triangles.

10. For point loads draw vertical lines and under udl draw slope lines linear

BENDING MOMENT

The bending moment at any section of the beam is defined as the algebraic sum of moments of all loads about the section by considering either left of that section or night of that section. It is denoted by the letter M and its units in SI system are KNm.

Sign Convention for Bending Moment:

Sagging or Positive Bending Moment: The bending moment at a section is considered to be positive when it causes convexity downwards lor concavity at top) such bending moment is called sagging bending moment or positive bending moment.

Hogging or Negative Bending Moment: The bending mome at a section is constidered to be negative when it causes conve upwards (or concavity at bottom), such bending moments is calle hoging bending moment or negative B.M

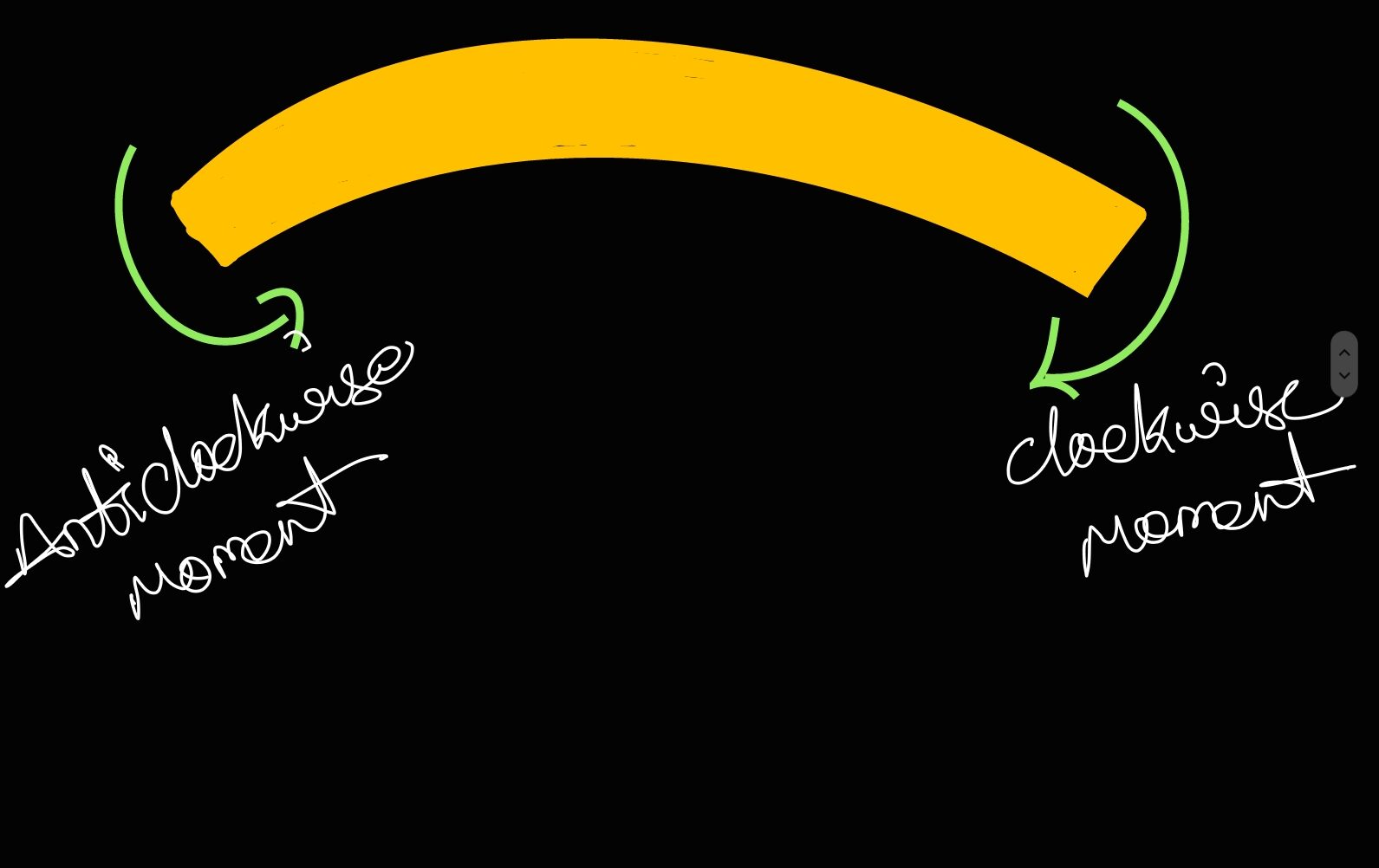
Bending Moment Diagram (BMD):

B.M.D. is a graphical representationatio of the values of bending moments plotted as ordinates on a

Procedure to be Followed for drawing B.M.D:

Calculate the B.M at different salient points with sign Le, +ve or ve

2. Draw the base line and plot the positive values of BM above the base and negative values of BM below the base line.

3. In between point Joods draw slope line and in between udi draw parabolic lines, and watch it properly.

4. Find the max +ve and max-ve BM values and its occurrence