Q. A Survey line ABDE intersects a building between Band D. To overcome the obstacle a perpendicular BC 90 m long, is set out at B. From C, two lines CD and CE are set out at angles 45º and 60 respectively with CB. Find the lengths CD and CE such that points D and E fall on the prolongation of line AB. Also find the obstructed distance BD.
solution
Given :
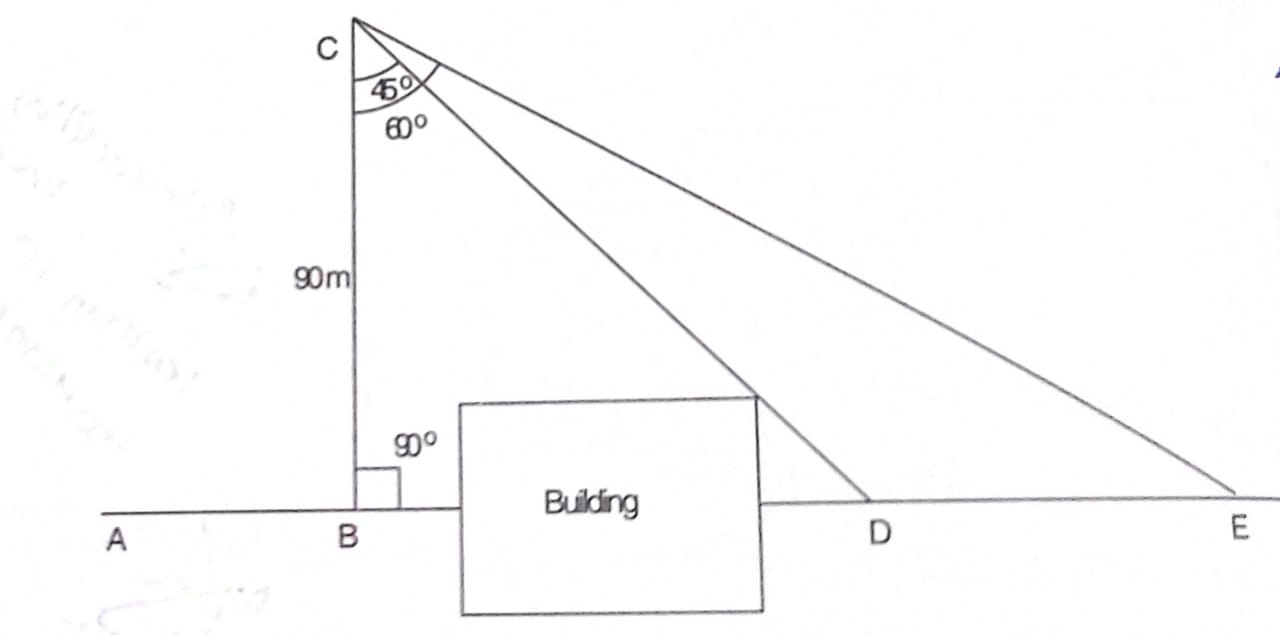
BC = 90 m
∠ BCD= 45°
∠BCE=60°
From ΔBCD,
COS 45° = BC/CD
Therefore CD= BC / cos 45°= 90/ cos 45º = 127.28 m
and tan 45° =BD/ BC
Therefore BD= BC tan 45°
= 90 x tan 45º
= 90m
Similarly, from ΔBCE,
cos 60° = BC / CE
therefore CE = (BC)/(cos 60°) = 90/(cos 60°) = 180m
Q. There is a tower “T”, on the other bank. A point ‘C’ is selecte opposite to the tower and ‘CB’ is set out right angles to the line CT at C’ with a optical square. Line BC is produced to ‘A’ and the angles CBT and CAT measured were 30° and 45°. If the length of the line AB = 210 m, find the width of the river.
Solution:
From the given problem first we can make a sketch. (Fig.)
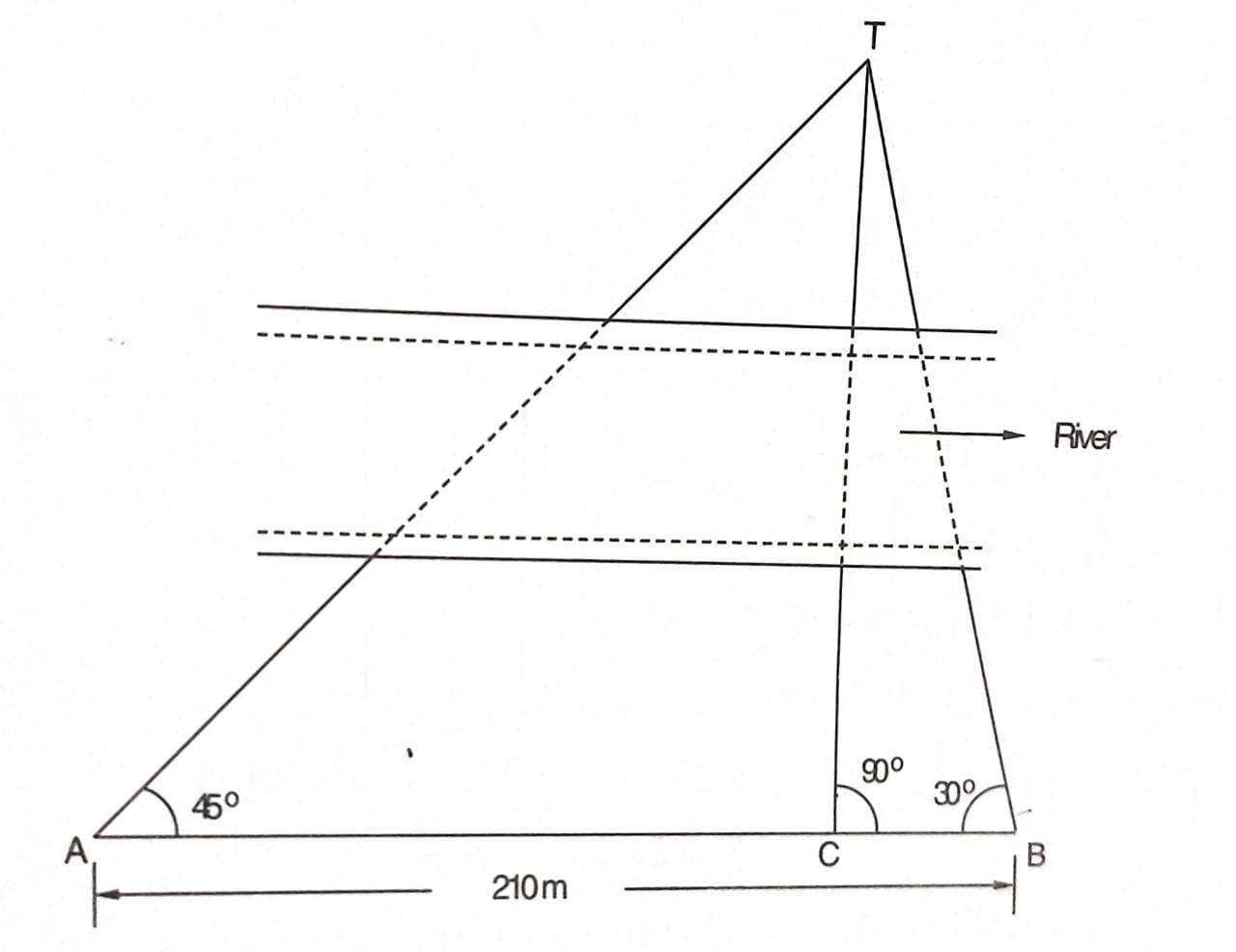
∠ CAT = 45° and. ∠ CBT = 30°
AB= 210 m
From ΔACT:
tan 45º = CT /AC
AC= CT / tan 45°
Now, from ΔBСТ,
tan 30° = CT/BC
BC= CT / tan 30°
By addition of the above equations (1) and
AC + BC = CT / tan 45° + CT / tan 30 °
= CT [ 1/tan. 45º + 1 / tan30°]
But AC + BC= AB =210 m
210m =CT(2.732)
CT=210/ 2.732 = 76.867 m
The width of the river = 76.867 m
Q. B and C are two points on opposite banks of a river along a chain line ABC. A line BD, 60 m long is set out at right angles to the chain line at B. Another line DE is set out at right angles to the line CD at D, such that the point ‘E’ is on the chain line and 90 m behind the point B. Find the width of the river.
Solution:
From the given problem, we can make a sketch
Given Data: BD = 60 m, BE = 90 m
CBD =90° and CDE = 90°
From Fig. ΔBCD andΔBDE are similar
FIG

Hence BC / BD =BD/BE
Therefore BC=BD/BE × BD
= BD²/ BE = 60 /90 = 40m
Width of the river ‘BC’ = 40 m
