Q.A survey line ABC crossing a river at right angles cuts its banks at B and C. To determine width of river BC, a line BE, 30 m long was set out roughly parallel to the river. A point D was found in CE produced and middle point of DB determined, EF was then produced to G, making FG equal to EF, and DG produced to cut the survey line in H. GH and HB were found to be 20 and 40 metres long respectively. Find the distance from B to C .
solution
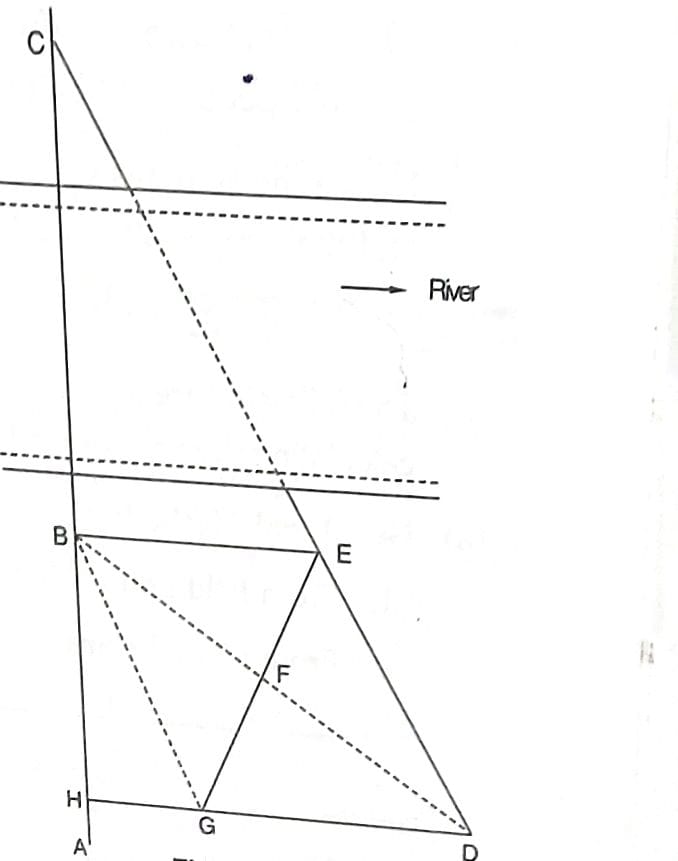
In Parallelogram BEDG
BF= FD and GF =EF
Hence GD= BE=30m
therefore HD=HG+GD
=20+30=50m
From Similar triangle CHD and CBE
we get
CB/BE = CH/HD or CB/ CH = BE/HD
or CB / CB+BH = BE / HG+ GD
or CB / CB +40 = 30/ 20+30
or CB/ CB+40 = 0.60
Or CB= 0.60 CB+24
CB (1–60) =24
or CB = 24 /0.40 = 60 m
Q.P and Q are two points 350 m apart on the same bank of river. The bearings of a tree on the other bank observed from P and Q, are 35° and 320°, respectively. Find the width of the river if bearing of PQ is 95°.
solution
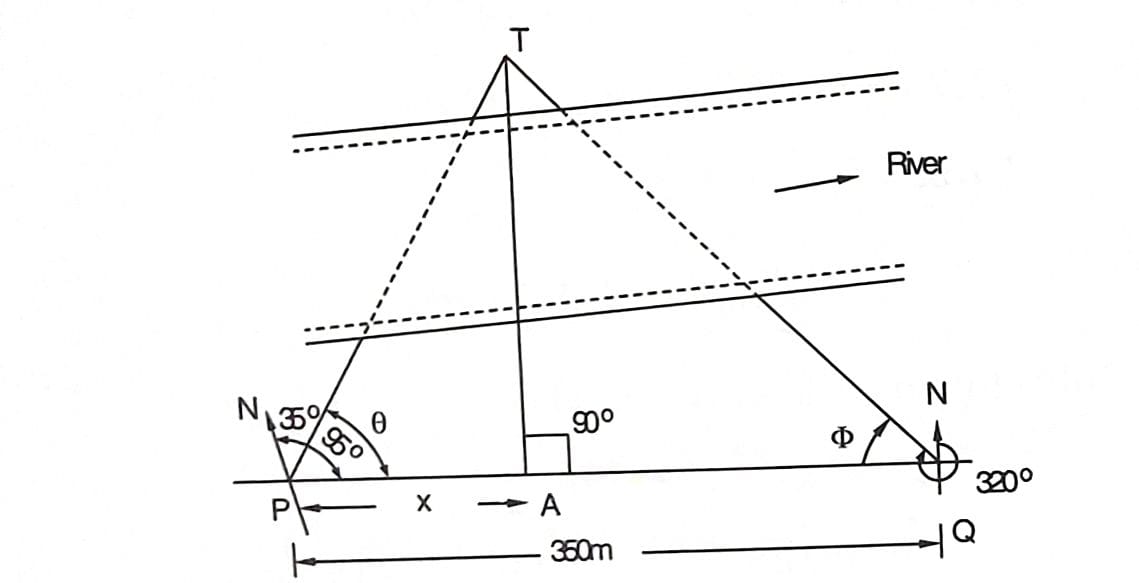
Let the points P and Q. be on the near side and the tree T on the far bank of the river. From ‘T draw a perpendicular TA to PQ .The TA is the width of the river.
Let PA = x
Then AQ = PQ – x = 350 – x
θ= bearing of PQ – bearing of PT
= 95° – 35° = 60°m
φ= bearing of QT – back bearing of PQ
= 320°- (180°+ 95°)
= 45 °
Now, from Δ PAT
tan θ = (TA)/(PA)
Substituting PA = x and θ= 60 deg TA = x tan 60°……..1
similarly from ΔQAT
tan φ= TA / AQ
substituting AQ= ( 350-x) and φ=45°……………2
solving Equation 1 and 2
x tan 60°= (350-x) tan 45°
X x 1.732 = ( 350-x) x 1.00
2.732 X = 350
X = 350/2.732= 128.11m
substitue X In Equation 1
TA= X tan 60°
= 128.11 x tan 60° . = 221.89m
Hence, coldth of the river is 221.89m
